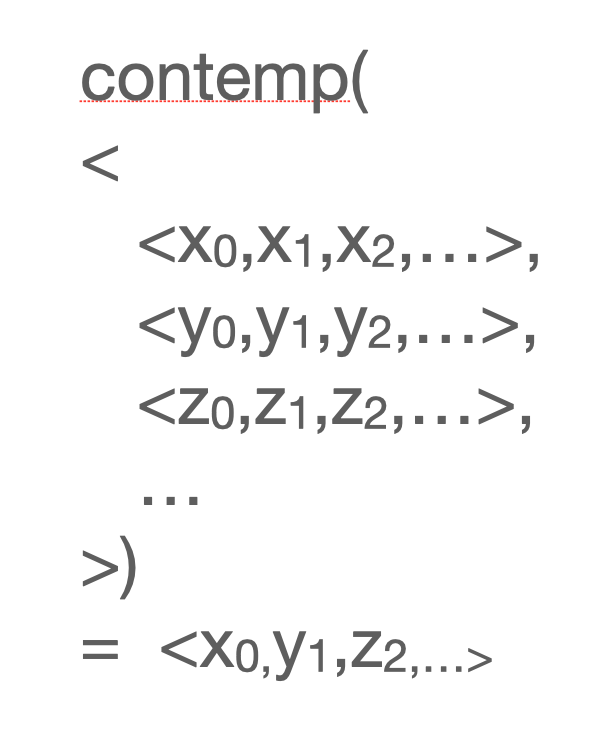When Ed Ashcroft and I invented Lucid, we intended it be a general purpose language like Pascal (very popular at the time.)

Pascal had while loops and we managed to do iteration with equations. However in Pascal you can nest while loops and have iterations that run their course while enclosing loops are frozen. This was a problem for us.

To see the problem consider the following Pascal-like program which repeatedly inputs a number, computes an approximation to its square root using Newton’s method, and prints it out

N = input() ;
while N ne eod
  a = 1 ;
  err = abs(N-1)
  while err > 0.0001
    a = (a+N/a)/2 ;
    err = abs(N-a*a) ;
  end
end

We can naively rewrite this as Lucid giving

output
where
  N = input;
  output =
  a așa err < 0.0001
  where
    a = 1 fby (a+N/a)/2
    err = abs(N-a*a)
  end;
end

All very good but it doesn’t work – it’s output is garbage. The problem is that N continues changing in sync with the approximation a. The Newton iteration is chasing a moving target and may not even terminate.

The difference between Lucid and Pascal is that with Pascal by default nothing changes whereas with Lucid everything changes by default.

Obviously, if Lucid wants to be a general purpose language it needs nesting. We needed some way to ‘freeze’ the current value of N while the inner loop is running. We came up with the “is current” declaration, an ad hoc solution.

The program becomes

output
where
  n = input;
  output =
  a așa err < 0.0001
  where
    N is current n;
    a = 1 fby (a+N/a)/2
    err = abs(N-a*a)
  end;
end

There were many problems with this solution, starting with the fact that N is no longer defined by an equation. The is current statement was unpopular with Lusers (Lucid users) and tended to be dropped. GLU did not have nesting and instead used temporary extra ‘throw away’ dimensions.

Can we do better? I think so, and I’m going to outline a proposal. The idea is to use operations (I call them”hyper filters”) that work on streams (I call them “hyperstreams”) that are functions of a whole sequence t₀,t₁,t₂,… of time parameters, not just t₀ as with ordinary streams. The idea is that t₀ is inner, local time, t₁ is time in the enclosing loop, t₂ time in the second outer loop, and so on.

I’m also going to correct original Lucid’s biggest mistake, which was to try to get away with only one type of where clause. The semantics were a mess. Instead we have a plain where clause which simply hides definitions, and whereloop, used for nesting. Then we’ll define whereloop in terms of a simple translation into conventional where.

I’m not satisfied with simply reviving the original simple ‘freezing’ form of nesting. I’m proposing a more general framework that allows, for example, several rounds of the inner loop to produce one value for the outer loop. This framework uses two general purpose multi (time) dimensional operators, active and contemp (orary).

Although these two hyperfilters act on infinite dimensional hyperstreams we can understand them in terms of one- and two- dimensional streams extended point wise to the other dimensions. A whereloop implicitly applies active to all its globals and contemp to its result.

The operator active takes a stream and duplicates it over t₀.

In other words, if a is the argument stream, active(a) repeatedly starts from scratch in each invocation of the inner loop.

The operator contemp, on the other hand, takes a two-dimensional stream and samples it.

In other words, if contemp(w) is the contemporary value of w, the value in the current enclosing time.

It’s easy to check that contemp and active are dual, that contemp(active(a)) = a.

If we want simple freezing we use the operator current, defined as

current(<g₀,g₁,g₂,…>) = <<g₀,g₀,g₀,…>,<g₁,g₁,g₁,…>,<g₂,g₂,g₂,…>,…>

The square root program becomes

output
where
  n = input;
  output =
  a așa err < 0.0001
  whereloop
    N = current n;
    a = 1 fby (a+N/a)/2
    err = abs(N-a*a)
  end;
end

After translating the whereloop we get

output
where
  n = input;
  output =
  contemp(a așa err < 0.0001)
  where
    N = current active(n);
    a = 1 fby (a+N/a)/2
    err = abs(N-a*a)
  end;
end

Inside the inner where n might look like <2,9,3,…>, active n will be

<<2,9,3,…>,<2,9,3,…>,<2,9,3,…>,…>

and current active n will be

<<2,2,2,…>,<9,9,9,…>,<3,3,3,…),…>

and now a is no longer chasing a moving target. The hyperstream a might look like

<<1,1.6666,1.478,…,1.414…,1.414…,>,<1,2.5,2.9,…,3,3,3,…>,<1,1.2..,1.6…,1.73…,1.73…,>,…>

and a așa err<0.0001 will be

<<1.414…,1.414…,1..414…,>,<3,3,3,…>,<1.73…,1.73…,1.73…,…>,…>

and v is

<1.414…,3,1.73…,…>

which is what we want.

So much for the simplest form of nesting, where outer values are frozen during the inner computation. Can we do better? Yes.

Suppose we want to produce a single value that repeatedly combines several values from the outer loop (not possible in traditional Lucid). To be specific, suppose that m is a series of positive integers interrupted by 0’s. We want to produce the stream of sums of the numbers up to each 0. For example, if m is of the form

<3,2,4,0,6,0,3,8,5,0,…>

then the value of the loop should be of the form <9,6,16,…>.

Here is the program

m
where
    n = input;
    m = 
    sum asa y eq 0
    whereloop
     sum = 0 fby sum+y;
     y = n Fby y after y eq 0;
    end;
end

It uses the (ordinary) filter after and the hyperfilter Fby. The former returns that part of its first argument after its second argument is true for the first time. For example, if P begins <f,f,f,t,…> and X begins <x₀,x₁,x₂,x₃,x₄,…> then X after P is <x₄,x₅,x₆,…>. The definition of after is

X after P = if first P then next X
             else first X fby next X after next P
            fi;

This is standard one dimensional Lucid. But Fby is two dimensional; it’s fby in the time dimension t₁. If V is <<x₀,x₁,x₂,…>,<y₀,y₂,y₃,…>,<z₀,z₁,z₂,…>,…> and W is <<a₀,a₁,a₂,…>,<b₀,b₁,b₂,…>,<c₀,c₁,c₂,…>,….> then V Fby W is

<<x₀,x₁,x₂,…>,<a₀,a₁,a₂,…>,<b₀,b₁,b₂,…>,<c₀,c₁,c₂,…>,…>

(Incidentally there does not seem to be any way to define Fby in terms of simpler primitives.)

Once we translate the whereloop we get

m
where
    m = input;
    n = 
    contemp(sum asa y eq 0)
    where
     sum = 0 fby sum+y;
     y = active(m) Fby y after y eq 0;
    end;
end

If m is as above then y is

<3,2,4,0,6,0,3,8,5,0,…>,<6,0,3,8,5,0,…>,<3,8,5,0,…>,…>

sum is

<<0,3,5,9,9,15,15,…>,<0,6,6,9,17,…>,<0,3,11,16,16,…>,…>

sum așa y eq 0 is

<<9,9,9,…>,<6,6,6,…>,<16,16,16,…>,…>

and contemp(sum așa y eq 0) is <9,6,16,…>, as required.

On the other end of the spectrum, we want a loop which produces a number of values for every step in the enclosing loop. Suppose that n is a stream of natural numbers, say <2,5,8,3,…> and we want to produce a stream m that enumerates the binary digits of the components of n separated by “;”, so that m will be of the form

<0,1,”;”,1,0,1,”;”,0,0,0,1,”;”,1,1,”;”,…>

The following program does the job

m
where
 n = input;
 m =
 (";" fby digit) Until (false fby k eq 0)
   whereloop
    k = current n fby k/2;
    digit = k mod 2;
   end;
end

The operator Until is defined recursively as

 x Until p = if First first p then (Next x Until Next p)    else First first x fby (next x Until next p) fi

Here First and Next are the t₁ versions of first and next.

Does this work? I believe so, but I leave it to you as a (nontrivial) exercise to check it. Let me know if it doesn’t work out.

It all looks hunky-dory but there is a problem: global functions. I explained that whereloop is translated by applying active to all the global (individual) variables. But what about a function f that is defined outside the whereloop but is called inside? The hitch is that the definition of f may contain a global g that normally should be active-ated. If we do nothing we end up ‘smuggling’ g inside the whereloop with unpredictable consequences because we have not turned it into a two dimensional stream.

We can’t just ignore global function calls. What do we do with them? We can try Yaghi code, which seems to work, but I’ll leave the details for a later time. In the meantime, there’s no problem using globally defined functions that have no globals.